FLAT EARTH VS. ROUND EARTH (Hyperbolic VS Spherical) by B. Potter

I often find myself irritated by the arguments of those around me. Black vs. White, Love Vs. Hate, Male Vs. Female, Creation Vs. Evolution. I explain my frustration by stating what I find to be true, both apparent opposites are the same thing, in variable intensity. Tonight, I would like to discuss the argument of FLAT EARTH VS ROUND EARTH, using geometry to discuss it. I argue that the answer is "YES" as both sides are saying the same thing ultimately, and arguing senselessly.

Flat Earth Vs. Round Earth

In the realm of geometry, two distinct branches have emerged to challenge our conventional understanding of space and shape - spherical geometry and hyperbolic geometry. These branches provide alternative frameworks to explain the Earth's seemingly contradictory nature of being both flat and round. Let's delve into the differences between these geometries and how they shed light on this intriguing concept.

Spherical geometry is a non-Euclidean geometry that deals with shapes on the surface of a sphere. It diverges from the traditional Euclidean geometry, which assumes a flat plane. In spherical geometry, lines are defined as great circles, which are the intersections of the sphere's surface with planes passing through its center. These great circles are analogous to straight lines in Euclidean geometry. One of the key characteristics of spherical geometry is that the sum of the angles of a triangle exceeds 180 degrees. This deviation from Euclidean geometry is a consequence of the curvature of the sphere's surface. For example, if we were to draw a triangle on the Earth's surface, with vertices at three cities, the sum of the angles would be greater than 180 degrees.

On the other hand, hyperbolic geometry is another non-Euclidean geometry that explores shapes with negative curvature. Unlike spherical geometry, hyperbolic geometry deals with shapes that are saddle-shaped. In this geometry, the sum of the angles of a triangle is always less than 180 degrees, highlighting the inherent curvature of hyperbolic space.

Now, let's explore how these geometries help us understand the Earth's seemingly contradictory nature. While the Earth appears flat when observed on a small scale, it is, in fact, a sphere when viewed on a larger scale. Spherical geometry explains the Earth's roundness, as it accurately represents the curvature of the planet's surface. However, when we examine a small portion of the Earth's surface, such as a city or a region, the curvature becomes negligible, and the surface appears flat. This local flatness aligns with our intuitive understanding of a flat Earth.

Hyperbolic geometry further adds to this understanding by demonstrating that a surface can be both flat and curved simultaneously, depending on the scale of observation. In essence, the Earth's flatness and roundness can be reconciled by considering the different scales at which we observe it. Spherical geometry explains the overall roundness of the Earth, while hyperbolic geometry helps us understand the local flatness experienced in our day-to-day lives.

To conclude, spherical geometry and hyperbolic geometry provide alternative mathematical frameworks to understand the Earth's seemingly contradictory nature of being both flat and round. Spherical geometry explains the Earth's overall roundness, while hyperbolic geometry sheds light on the local flatness observed in smaller scales. By exploring these geometries, we can appreciate the intricate mathematical train of thought that helps us comprehend the complex nature of our planet.

STOP ARGUING YOU'RE BOTH RIGHT! THE FIRMAMENT IS CALLED AN ATMOSPHERE NOW AND IT IS MOST DEFINITELY THERE! <3

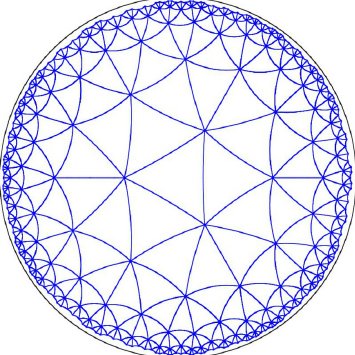
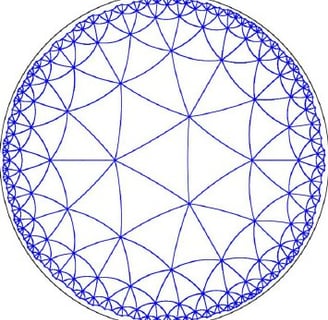
Hyperbolic Flat Earth Geometry

Spherical Round Earth Geometry